Hello! When doing Time Series Forecasting (ARIMA), the TS needs to be made stationary if it is not. My understanding is that Exploratory relies on the (augmented) Dickey-Fuller test for that. If the order of differencing is ‘0’ after the forecast is run, does that mean the time series was stationary in the first place and no differencing occurred? Thanks!
Yes, if the order of differencing is 0 and the order of seasonal differencing is also 0, that means the original data was stationary in the first place.
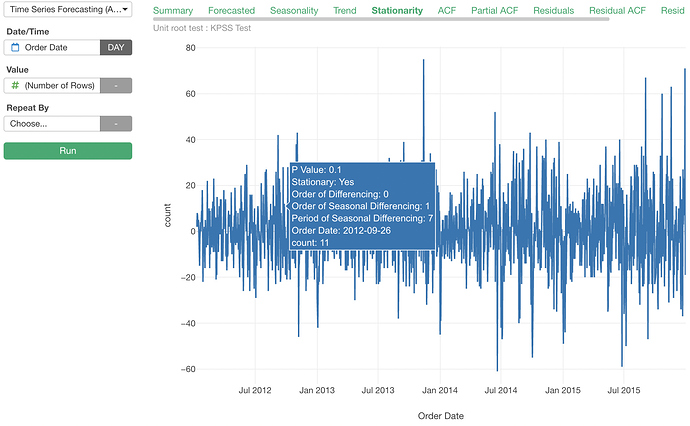
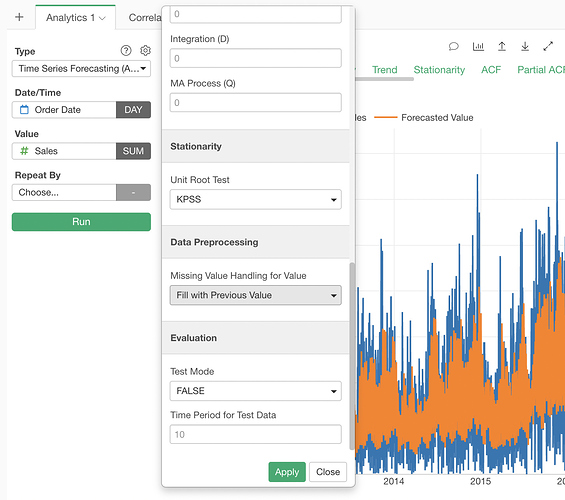
Note that ARIMA on Exploratory tries seasonal differencing (weekly or yearly depending on the unit of time) too by default. So it is also possible that even the order of differencing is 0, the order of seasonal differencing may not be 0, and in that case, ARIMA applied seasonal differencing to make the series stationary. You can check that on the Summary tab (d is the order of differencing, and D is the order of seasonal differencing.), or on the hover balloon on the Stationarity tab.
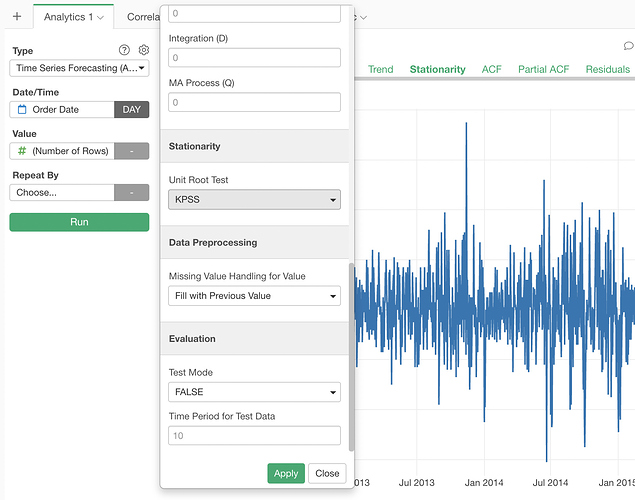
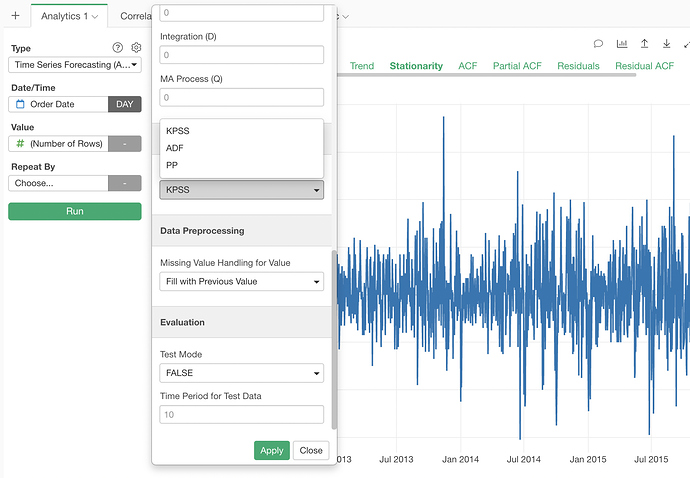
By the way, the stationarity test used by default is KPSS. You can select the Augmented Dickey-Fuller test in the Property dialog.
Thank you, Hideaki, this is a great answer! I appreciate the you pointing out the differences between differencing and seasonal differencing. Related to that, Exploratory seems to handle irregular time series ok. How is an uneven/irregular sampling frequency accounted for?
Hi Rob!
The data is by default preprocessed into a regular time series without missing values.
It’s done in 2 steps.
- Aggregation
The data is aggregated for each period, making it a regular time series.
The period and the aggregation function can be specified here.
- Filling the missing values
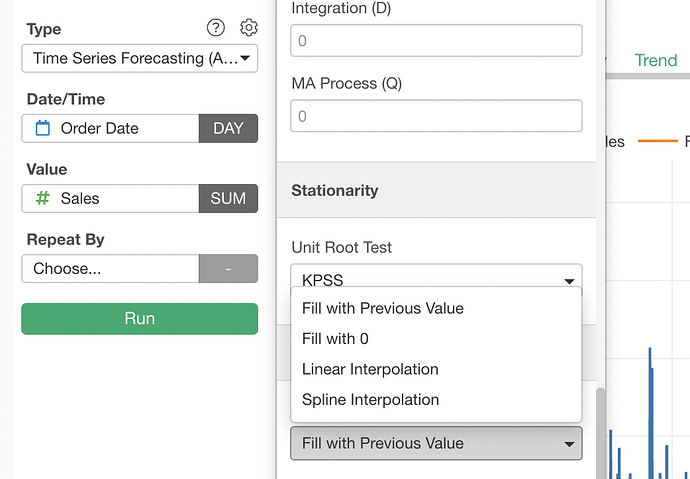
For ARIMA to be able to work on the data, the missing values need to be filled.
By default, it is done by filling with the previous non-NA value. You can select the NA filling logic from the options in the Property dialog.
Perfect, I see that now, Hideaki - thank you!